(17.1-17.2)项目实战:多机lnmp部署
本文共 1826 字,大约阅读时间需要 6 分钟。
文章目录
安装tengine+php
main.sh将整个文件夹lnmp推到不同的服务器上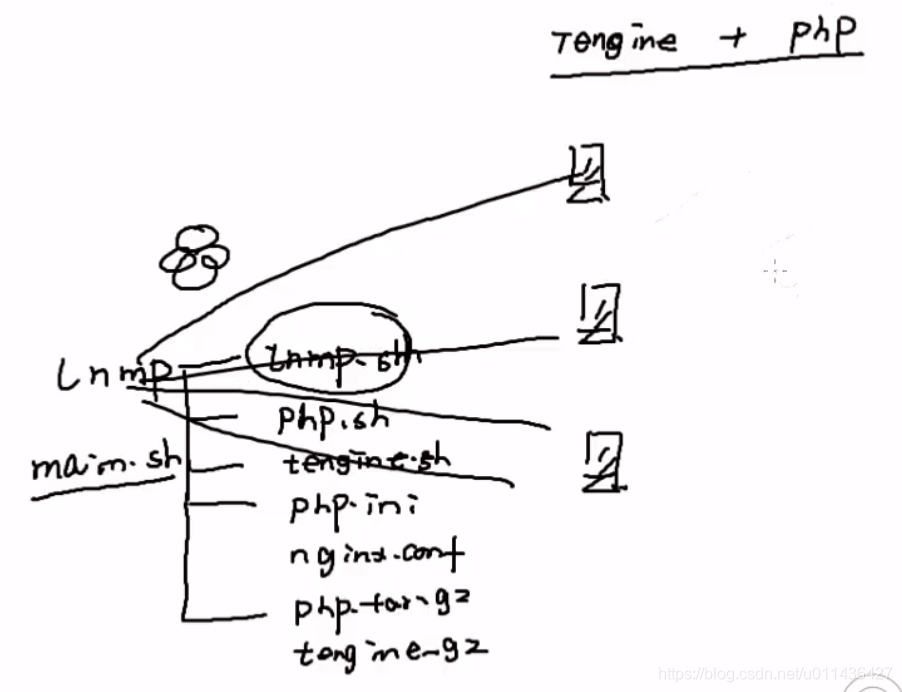
- 获取安装包
从172.16.8.100服务器获取php.tar.xz和tengine.tar.gz这两个包lftp 172.16.8.100cd source-softget php.tar.xz tengine.tar.gzby
-
yum install -y tree
tree可以看到目录结构,执行的是lnmp.sh脚本:它会调用一切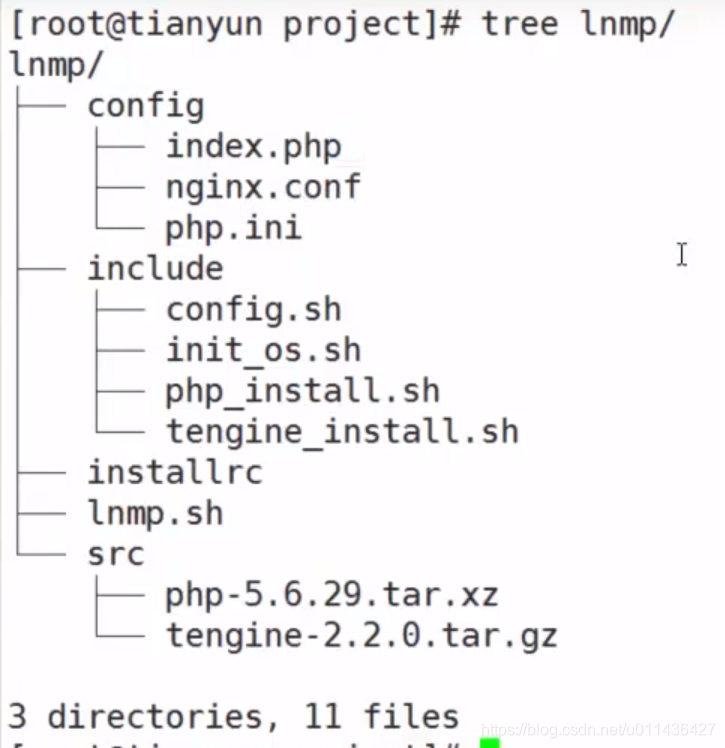
-
lnmp.sh脚本
#!/usr/bin/env bash#inmp installsoft_dir=`pwd`/srcconfig_dir=`pwd`/configcpus=`lscpu|awk '/^CPU\(s\)/{print $2}'`. installrc. include/init_os.sh. include/tengine_install.sh. include/php_install.sh. include/config.shinit_ostengine_installphp_installconfig - init.sh,该脚本放在include目录下面
#!/usr/bin/env bash#init os
- install_php.sh
#!/usr/bin/env bashphp_install(){ yum -y install libjpeg libjpeg-devel libpng libjpeg-devel freetype freetype-devel \ libxml2 libxml2-devel libcurl libcurl-devel libxslt-devel openssl-devel cd ${ soft_dir} tar xf ${ php_version} cd ${ php_version%.tar.xz} ./configure \ --prefix=${ php_prefix} \ --with-curl \ ... ... --enable-xml \ --enable-zip make -j ${ cpus} make install ##php-fpm配置文件:影响php处理php程序的性能,例如php进程数,最大连接数配置等 cp ${ php_prefix}/etc/php-fpm.conf.defaul ${ php_prefix}/etc/php-fpm.conf ##php配置文件:影响phph代码,eg:允许客户端最大上传文件的大小,php扩展功能是否可以连接MySQL,MEMcache等 cp php.ini-production /usr/local/php/lib/php.ini ##添加到init启动项 cp sapi/fpnfpm/init.d.php-fpm /etc/rc.d/init.d/php-fpm chmod a+x /etc/rc.d/init.d/php-fpm chkconfig --add php-fpm chkconfig php-fpm on service php-fpm start} - intstallrc
#!/usr/bin/env bash#installrctengine_version=tengine-2.2.0.tar.gzphp_version=php-5.6.29.tar.xztengine_prefix=/usr/local/tenginephp_prefix=/usr/local/phpnginx_prefix=/usr/local/nginx
- configure.sh
#!/usr/bin/env bashconfigure(){ ##放置替换文件时的提示,可以在cp前面加上转移\ \cp ${ config_dir}/nginx.conf ${ nginx_prefix}/conf/nginx.conf \cp ${ config_dir}/index.php ${ nginx_prefix}/html/index.php ${ nginx_prefix}/sbin/nginx /etc/init.d/php-fpm restart} 

- include/index.php
转载地址:http://cjfzz.baihongyu.com/
你可能感兴趣的文章
MySQL:什么样的字段适合加索引?什么样的字段不适合加索引
查看>>
MySQL:判断逗号分隔的字符串中是否包含某个字符串
查看>>
MySQL:某个ip连接mysql失败次数过多,导致ip锁定
查看>>
MySQL:索引失效场景总结
查看>>
Mysql:避免重复的插入数据方法汇总
查看>>
MyS中的IF
查看>>
M_Map工具箱简介及地理图形绘制
查看>>
m_Orchestrate learning system---二十二、html代码如何变的容易
查看>>
M×N 形状 numpy.ndarray 的滑动窗口
查看>>
m个苹果放入n个盘子问题
查看>>
n = 3 , while n , continue
查看>>
n 叉树后序遍历转换为链表问题的深入探讨
查看>>
N!
查看>>
N-Gram的基本原理
查看>>
n1 c语言程序,全国青少年软件编程等级考试C语言经典程序题10道七
查看>>
Nacos Client常用配置
查看>>
nacos config
查看>>
Nacos Config--服务配置
查看>>
Nacos Derby 远程命令执行漏洞(QVD-2024-26473)
查看>>
Nacos 与 Eureka、Zookeeper 和 Consul 等其他注册中心的区别
查看>>